İstatistik – KPSS Ders Notu
Bu yazıda neler okuyacaksınız?
- İSTATİSTİK
- A. TEST PLANI
- B. VERİLERİN DÜZENLENMESİ
- C. TEST ANALİZLERİ
- D. MADDE ANALİZLERİ
Ölçme ve Değerlendirme KPSS ders notlarının son kısmında İstatistik konusu ile devam ediyoruz. Bu konu kapsamında İstatistik nedir?, Test planı, verilerin düzenlenmesi, test analizleri, madde analizleri konularına ve alt başlıklarına değineceğiz.
İSTATİSTİK
A. TEST PLANI
- Sınavın amacı belirlenir.
- Ölçülecek davranışlar belirlenir.
- Belirtke tablosu hazırlanır.
- Kullanılacak soru tipine karar verilir.
- Denemelik maddeler yazılır.
- Denemelik maddeler test düzenine konur.
- Denemelik test uygulanır.
- Madde analizi ile madde seçilir.
- Nihai test uygulanır.
- Test istatistikleri yapılır.
NOT
- Eğer öğrencilerin, sınıfın, grubun başarıları karşılaştırılıyorsa merkezi eğilim ölçüleri,
- Eğer bir öğrencinin grubuna/sınıfına göre bağıl başarısı soruluyorsa standart puanlar (Z-T)puanı,
- Eğer öğrencilerin farklılaşma, homojenlik, heterojenlik düzeyi karşılaştırılıyorsa merkezi dağılım ölçüleri kullanılır.
- Eğer testteki soruların zorluğu, ayırt ediciliği, güvenirliği soruluyorsa madde analizleri kullanılır.
B. VERİLERİN DÜZENLENMESİ
1. PUANLARIN SIRAYA KONMASI
- Bir testten elde edilen puanlar büyükten küçüğe ya da küçükten büyüğe sıralanır.


2. PUANLARIN FREKANS TABLOSUNU OLUŞTURMA
- ÖĞRENCİ- FREKANS TABLOSUNDA , öğrencilerin almış oldukları puanlar büyükten küçüğe doğru sıralanır.


BU TABLODA;
- Sınıf mevcudu bulunur.
- Hangi puanı kaç öğrencinin aldığı bulunur.
- Frekans sayılarının toplamı = sınıf mevcudu olarak belirlenmiş olur.
- Tablodaki sınıf mevcudu = 50 kişiden oluşmaktadır.
- TOPLAMALI FREKANS = TOPLAM FREKANS = SINIF MEVCUDU
ÖRNEK 1: Tabloya göre , sınıf mevcudu nedir ?


CEVAP: Frekansları toplayarak mevcudu bulabiliriz. 5+3+2+4= 14 kişi
ÖRNEK 2: Tabloya göre, yığılmalı frekans nedir?


CEVAP: Toplamalı frekans yani yığılmalı frekansı bulmak için ilk frekansla sonraki frekans toplanarak ilerlenir.


ÖRNEK 3: Tabloya göre , sınıf mevcudu nedir ?


CEVAP: 1+5+4+3= 13 kişi
C. TEST ANALİZLERİ
A. MERKEZİ EĞİLİM(YIĞILMA) ÖLÇÜLERİ
1. ARİTMETİK ORTALAMA
- Puanlar toplamının, puan sayısına bölünmesidir.
NOT
- Aritmetik ortalama, dağılımdaki uç değerlere duyarlı olduğundan, uç değerlere doğru sapar.
- Uç değerlerin olduğu dağılımlarda (çarpık dağılımlarda) aritmetik ortalama iyi bir merkezi eğilim ölçüsü değildir.
- Uç değerlerde en iyi merkezi eğilim ölçüsü, medyandır.
- Ancak simetrik dağılımlarda uç değerler olmadığı için aritmetik ortalama, daha kullanışlı ve güvenilirdir.
- Aritmetik ortalama, en çok bilgi içeren veri olduğundan grup başarısında kullanılır.
ÖRNEK: Bir tarih testinden 6 kişinin aldığı puanlar şöyledir: 7,2,5,3,9,4 Buna göre tarih testinin aritmetik ortalaması kaçtır ?
7+2+5+3+9+4=30, 6 kişi olduğundan aritmetik ortalama 30/6=5 olarak bulunur.
ÖRNEK: Tablonun aritmetik ortalaması kaçtır?


Önce frekansları değerlendiriyoruz. 2 kişi 20, 2 kişi 40 ve 2 kişide 60 almış. O zaman 20+20+40+40+60+60=240 6 kişi olduğundan 240/6=40 olarak aritmetik ortalamayı bulabiliriz.
ÖRNEK: Tabloda verilen puan aralığının aritmetik ortalaması kaçtır?


- Puan aralıklı aritmetik ortalama sorularında puan aralığının ortalaması alınır.
- 0-6 puan aralığı bize 3 değerini vermektedir.
- 8 kişi 3 puan, 6 kişi 10 puan, 4 kişi 17 puan, 2 kişi 24 puan ve 1 kişi 31 puan almıştır.
- (8×3)+(6×10)+(4×17)+(2×24)+(1×31) = 231 yapar, ardından kişi sayısına bu sayıyı bölüyoruz; 231/21=11 olacaktır.
DİKKAT!
- Grupların mutlak başarıları soruluyorsa Aritmetik Ortalamaya bakılır.
- Gruplara sorulan sorular eşitse sadece Aritmetik Ortalamaya bakılır.
Gruplara sorulan sorular eşit değilse ; Testlerin ortalama güçlükleri belirlenir.
Test Ortalama Güçlüğü = Aritmetik Ortalama / K (K= soru sayısı)
YORUM: Elde edilen değerler: (0 ve 1 aralığında değer alır.)
- 0.40 test zor, grup başarısız
- 0.40-0.60 test orta güçlükte
- 0.60-1 test kolay ,grup başarılıdır.
DİKKAT: Eğer maddelerin güçlük indeksi verilip, aritmetik ortalama istenirse :
GÜÇLÜKLER TOPLAMI= ARİTMETİK ORTALAMA olur.
ÖRNEK 1: Tabloya göre grubun en başarılı olduğu test ?


Tabii ki aritmetik ortalamanın en büyük olduğu test olan 2. test cevap olacaktır.
ÖRNEK 2: Tabloya göre grubun en başarılı olduğu test hangisidir?


Yine cevabımız aritmetik ortalamanın en yüksek olduğu 5. test olacaktır.
ÖRNEK 3: Tabloya göre en başarılı olunan test hangisidir?


- Bu soruda dikkat edilmesi gereken şey soru sayılarıdır. Soru sayıları farklı olan testlerde aritmetik ortalama kıyaslaması yapılırken soru sayıları ve aritmetik ortalamalar eşitlenir.
- Kolaylık olması açısından ben soru sayılarını 100’de buluşturmayı tercih ediyorum.
- 1. test için 40*2.5 yaparak soru sayısını 100 yapabilirim. Aynı işlemi aritmetik ortalamaya da yapamam gerekir o zaman 20*2.5 yapacağız. 1. test= 100 soruda 50 puanlık aritmetik ortalamaya sahip olacaktır.
- 2. test; 40*2.5= 100 soruda 75 puan olacak.
- 3. test; 100 soru 60 puan
- 4. test; 75*1.3=100 soru ve 78 puan olacak.
- 5. test 50*2=100 soru ve 30 puan olacak.
- Bu durumda en başarılı test 4. test olacaktır.
ÖRNEK 4: Tabloya göre aritmetik ortalama kaçtır ? (2017 KPSS)


Yapmamız gereken tek şey burada güçlükleri toplamak olacaktır. Biliyoruz ki madde güçlük indekslerinin toplamı bize aritmetik ortalamayı verir.
0.3+0.8+0.2+0.8+0.5= 2,6 olarak aritmetik ortalamayı buluruz.
1.2. AĞIRLIKLI ORTALAMA
- Puanların ortalamaya katkı düzeylerinin farklı olduğu durumlarda ağırlıklı ortalamadan faydalanılır.
ÖRNEK 1: Tabloya göre ağırlıklı ortalama kaçtır ?


- Ağırlıklı Ortalama = 4*70+4*60+4*80+3*50+3*60+3*75+3*85 = 1650
- 1650/24(Toplam Kredi sayısı) = 68,75 olarak ağırlıklı ortalamayı bulabiliriz.
2. MOD (TEPE DEĞER)
- Bir grupta en çok tekrarlayan puandır.
- Bir puan dağılımında birden fazla mod bulunabilir.
- İki tane mod varsa, çift modlu denir.
- İkiden fazla ise , çok modlu denir.
- Frekanslar eşitse, modsuz dağılım vardır.
- Bir dağılımda çift ya da çok modlu denilebilmesi için değerlerin art arda gelmemesi gerekir.
ÖRNEK 1: Tabloya göre mod nedir ?


Frekanslar eşit olduğundan bu tabloda modsuz dağılım olduğunu söyleyebiliriz.
ÖRNEK 2: Tabloya göre mod nedir ?


En çok tekrar eden puan 40 olarak görünmekte (9 kez). Bu da modun 40 olduğunu gösterir.
ÖRNEK 3: Tabloya göre mod nedir ?


30 puandan 8, 40 puandan 8 kişi bulunmaktadır. Çift moddan bahsedebiliriz. Mod 30 ve 40 puandır.
ÖRNEK 4: Tabloya göre mod nedir ?


Bu tabloda çok modlu bir sonuçla karşılaşıyoruz. 30, 55 ve 65 moddur.
ÖRNEK 5: Tabloya göre mod nedir ?


Yığılmalı frekansları önce inceleyip normal frekansları bulalım; 5-3-6-4 şeklinde bir frekans dağılımı olacaktır. 6 frekansın işaret ettiği 50 puan mod değerimiz olacaktır.
3. MEDYAN (ORTANCA)
- Bir puan dağılımını ikiye bölen puandır.
- Puanların yarısı bu puanın üstünde, diğer yarısı ise bu puanın altında yer almaktadır.
NOT: Ortalamayı çarpıtan uç değerlerde merkezi eğilim ölçülerinde medyan, merkezi dağılım ölçülerinde çeyrek sapma kullanılır.
NOT: Toplam Frekans Tek ise: N+1/2 sıradaki kişinin aldığı puan, medyandır.
NOT: Toplam Frekans Çift ise : N/2 Sıradaki kişinin aldığı puan, medyandır.
ÖRNEK 1: Tablonun medyanı nedir ?


- Bu soruda önce puanları büyükten küçüğe ya da küçükten büyüğe göre sıralamalıyız.
- 10,10,10,30,30,45,50,50,50,50,125,125,125,125
- İkinci adımda frekansları topluyoruz (kişi sayısını bulmak için) 3+4+2+1+4=14
- Frekans toplamları çift olduğundan N/2 formülünden medyan değerinin sırasını bulabiliriz. 14/2=7
- 7. değerin işaret ettiği puan (baştan ve sondan bakıldığında) 50 puan olarak karşımıza çıkıyor.
- Medyan 50.
ÖRNEK 2: Tablonun medyanı nedir ?


- Yığılmalı frekansı normal frekansa çevirelim; 3-2-3-6-12 bu da bize şu şekilde puan sıralaması yaptıracaktır;
- 15,15,15,20,20,30,30,30,40,40,40,40,40,40,50,50,50,50,50,50,50,50,50,50,50,50 toplam frekansımız 26; 26/2=13. sıradaki puan medyan değerimiz olacak. Baştan ve sondan saymaya başladığımızda baştan 13. değer ve sondan 13. değer 40 puanı göstermektedir.
- Medyan 40 olacaktır.
ÖRNEK 3: Tablonun medyanı nedir ?


- Daha önce puan aralığı ile aritmetik ortalama bulmuştuk. Aynı mantığı uygulayarak başlıyoruz.
- 2 kişi 6+0=6, 6/2=3 puan almıştır. Bu sisteme göre diğerlerini de yazıp sıraya dizelim. 3,3,10,10,10,10,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,24,24,24,24,24,24,31,31 dizilimini yapıyoruz.
- 32 kişilik bir grup olduğundan 32/2=16 medyan değerimiz olacaktır. 16. sıraya baştan ve sondan bakıyoruz ve 17 puanı işaret ettiğini görüyoruz.
- Medyan 17
B. ÇARPIKLIK ve ÖZELLİKLERİ
- Tek bir grubun başarı yorumunda kullanılan değerdir.
- Bir testin bir gruba kolay yada zor geldiği hakkında bilgi verir.
NOT: Birden fazla grup ise Testin Ortalama Güçlüğüne bakılarak karar verilir.
ÇARPIKLIK DEĞERİ = 3*( ARİTMETİK ORTALAMA – MEDYAN ) / STANDART SAPMA formülü ile bulunabilir.
ÇARPIKLIK DEĞERİ | TESTİN GÜÇLÜĞÜ |
| Pozitif | ZOR |
| Negatif | KOLAY |
| 0.10’dan küçükse | HAFİF ZOR |
| 0.10- 0. 25 arası | ORTA ZOR |
| 0.25’ten büyükse | ÇOK ZOR |
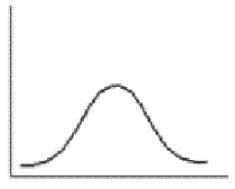
1. NORMAL (SİMETRİK) DAĞILIM
- Normal dağılım kalitesi en yüksek eğridir.
- Bu dağılımda MOD = MEDYAN = ARİTMETİK ORTALAMA şeklinde bir eşitlikten bahsedebiliriz.
- Bu testin uygulandığı grubun %50’si ortalamadan yüksek puan alır, %50’si ortalamadan düşük puan alır.
- Test , orta güçlüktedir.
- Öğrencilerin yarısı hedefe ulaşmıştır, yarısı hedefe ulaşamamıştır.
- En ayırıcı testlerdir. ➢Başarı testlerinin dağılımı bu şekilde olmalıdır.
- Eğitimde grubun başarı eğrisinin simetrik olması istenir.
- Ters simetrik dağılımların standart sapma ve varyansı, simetrik dağılımdan fazladır.

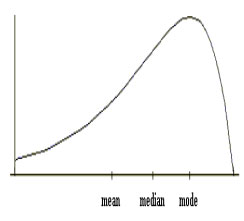
2. SAĞA ÇARPIK DAĞILIM
- Normal dağılım gösteren bir gruba diğerlerinden aşırı uçta puan ya da puanların eklenmesiyle oluşur.
- Sağa çarpık = Sola yığılmalı = Sağa kayışlı da denilir.
- A.O > MEDYAN > MOD şeklinde bir ilişki vardır.
- Test ve maddeler zordur.
- Bu testler seçme testleridir.
- Öğrencilerin büyük çoğunluğu hedefe ulaşamamıştır.
- Öğrencilerin çok azı hedefe ulaşmıştır.
- Bu öğrenciler grubun gruptaki en iyi öğrencilerdir.
- Alımların az başvuruların fazla olduğu durumlarda test zor olması istenir, grubunda sağa çarpık olması istenir.


3. SOLA ÇARPIK DAĞILIM
- Normal dağılım gösteren bir gruba diğerlerinden aşırı uçta puan ya da puanların eklenmesiyle oluşur.
- Sola çarpık = Sağa yığılmalı = Sola kayışlı da denir.
- MOD> MEDYAN > A.O şeklinde bir ilişki vardır.
- Test ve maddeleri kolaydır.
- Bu testler izleme testleridir.
- Öğrencilerin çoğu hedefe ulaşmıştır.
- Öğrencilerin çok azı hedefe ulaşamamıştır.
- Hedefe ulaşamayan öğrenciler, grubun en başarısız öğrencileridir.
- Tam öğrenme (Bloom) modelinin de dağılımı böyledir.

C. MERKEZİ DAĞILIM (YAYILIM) ÖLÇÜLERİ
- Grup ya da grupların farklılaşması, homojenliği / heterojenliği bulunmak istenildiğinde kullanılan değerdir.
- RANJ
- STANDART SAPMA ve VARYANS
- BAĞIL DEĞİŞKENLİK KATSAYISI
- ÇEYREK SAPMA
1. RANJ
- Bir dağılımda en büyük puan ile en küçük puan arasındaki farktır.
- Eğer dağılımdaki farklılaşma düzeyi hakkında çabuk bilgi edinmek istenildiğinde kullanılır.
- Ranj, uç değerlere duyarlıdır.
- Aradaki değerlere duyarlı değildir.
RANJ BÜYÜKSE;
- Grup heterojen,
- Bilenle bilmeyen ayırt edilebilir,
- Geçerlik ,güvenirlik yüksektir.
RANJ KÜÇÜKSE;
- Grup homojen,
- Bilenle bilmeyen ayırt ediciliği düşüktür,
- Geçerlik ,güvenirlik düşüktür.
ÖRNEK 1: Ranjı bulunuz.


Yapılacak işlem oldukça basit aslında en büyük değer olan 25’ten en küçük değer olan 5’i çıkarıyoruz. 25-5=20.
Ranj değeri 20’dir.
RANJ,
- Alınabilecek en yüksek puanın yarısından büyükse ranj geniş, grup heterojen, dağılım basık
- Alınabilecek en yüksek puanın yarısından küçükse ranj dar, grup homojen, dağılım sivri
- Alınabilecek en yüksek puanın yarısına eşitse grup, normal dağılım gösterir.
ÖRNEK 1: Sınav 100 puan üzerinden yapılıyorsa ; En Yüksek Puan = 67 , En Düşük Puan =65 ise grubun ranjı ve grup yapısı için ne söylenir ?
- 67-65=2, demek ki ranj değeri 2 olacaktır. alınabilecek en yüksek puan 100, 100/2=50 alınabilecek en yüksek puanın yarısıdır.
2<50 olduğuna göre; Ranj dar, grup homojen, dağılım sivridir.
ÖRNEK 2: En Küçük Puan: 15 En Büyük Puan: 50 Alınabilecek En Yüksek Puan: 60 Grubun ranj ve dağılım hakkında ne söylenebilir?
- Alınan en yüksek puandan, en düşük puanı çıkarıyoruz; 50-15=35.
- Alınabilecek en yüksek puanın yarısını bulalım; 60/2=30
- 35>30 yani Ranj değerimiz alınabilecek en yüksek puanın yarısından daha büyük.
- Ranj büyükse şu yorumları yapabiliriz; ranj geniş, grup heterojen, dağılım basık
2. STANDART SAPMA ve VARYANS
- Bir grubun sahip olduğu aritmetik ortalamaya öğrenci puanlarının yakınlık ya da uzaklığına standart sapma denir.
- Birden fazla grubun farklılaşması (homojenlik-heterojenlik ) sorulduğunda standart sapma kullanılır.
- Bir grupta ortalamaya uzak puan alan kişilerin, standart sapmaya katkısı fazladır. Bu nedenle standart sapma, uç değerlerden çok fazla etkilenir.
Normal dağılım gösteren bir grupta standart sapma ya da standart sapma değerinin karesi olan varyans değeri büyükse;
- Grup ölçülen özellik bakımından heterojen,
- Öğrenci puanları birbirinden uzak,
- .Grubun farklılaşma seviyesi fazla,
- Öğrencilerin öğrenme düzeyleri birbirinden farklı,
- Bilen ve bilmeyen ayrımı yapılabilen,
- Ayırt ediciliği yüksek,
- Güvenirliği ve geçerliği yüksek puanlardır.
Normal dağılım gösteren bir grupta standart sapma ya da standart sapma değerinin karesi olan varyans değeri küçüldükçe;
- Grup ölçülen özellik bakımından homojen,
- Öğrenci puanları birbirine yakın,
- Grubun farklılaşma seviyesi az,
- Öğrencilerin öğrenme düzeyleri aynı,
- .Bilen bilmeyen ayrımının zor,
- Ayırtediciliği düşük,
- Güvenirliği ve geçerliği düşük puanlardır.
NOT: Varyansın yorumu, standart sapma ile aynıdır. Varyans, standart sapmanın karesidir.
ÖRNEK: Tabloda 5 farklı testten elde edilen istatistikler verilmiştir. Uygulanan bu testlerdeki puanlama sistemleri birbirine eşittir.
A)Tabloda en homojen test puanları hangi testten elde edilmiştir?
B)Tabloda en heterojen test puanları hangi testten elde edilmiştir?


- Standart sapması en düşük olan 4. testte en homojen puanlar elde edilmiştir.
- Standart sapması en yüksek olan 1. testte en heterojen puanlar elde edilmiştir.
UYARI: Testlerden elde edilen puanların farklılaşma düzeylerinin karşılaştırılmasında testlerdeki her bir sorunun puan değeri eşitse (puanlama sistemleri) yalnızca standart sapmaya bakmak yeterlidir.
ÖRNEK 2: Tabloda farklılaşma en fazla hangi testte görülmektedir?


- Yine soruda farklılaşma düzeyinden bahsediliyorsa standart sapmalara bakarak karar vermeliyiz. Yalnız dikkatli olmamız lazım, soru sayıları farklı testleri inceliyoruz. Daha önce bu tarzda bir şeyle karşılaşmıştık. Soru sayılarını ortak paydada eşitlerken diğer değerleri de aynı oranda artırmalıyız.
- Kolaylık olması açısından soru sayılarını 100’de buluşturmayı tercih edeceğim.
- 1. Test: 100 soru – Standart sapma: 5
- 2. Test: 25*4=100 soru – Standart sapma: 3*4=12
- 3. Test: 50*2=100 – 4*2=8
- 4. Test: 30*3,3=99 – 6*3,3= 19,8
- 5. Test: 40*2,5=100 – 5*2,5=12,5 tüm bu değerleri incelediğimizde standart sapması en yüksek olan 4. test farklılaşmanın en fazla olduğu testtir.
UYARI: K (Soru Sayısı) farklı, eşitlendikten sonra puanlama sistemi aynılaştığından yapılacak yorum doğru olur.
3. BAĞIL DEĞİŞKENLİK KATSAYISI
- Tek bir grubun farklılaşması, homojenliği-heterojenliği kullanılır.
- Bir grubun basıklığı, sivriliği, normalliği hakkında bilgi verir.
V : Bağıl Değişkenlik Katsayısı
Sx : Standart Sapma
A.O : Aritmetik ortalama
Bağıl Değişkenlik Katsayısı (V) = Sx*100 / Aritmetik Ortalama
YORUM:
- 0-19 (HOMOJEN- SİVRİ )
- 20-25 (NORMAL )
- 26 ve üstü ( HETEROJEN – BASIK )
ÖRNEK: Bir grubun ortalaması 25, standart sapması 4 olduğuna göre dağılımın farklılaşma durumu ne olur ?
- Standart sapma 4’müş. Aritmetik ortalama ise 25.
- 4*100= 400, 400/25= 16
- O zaman yorumumuz 0-19 arasına göre yapacağız: Homojen – Sivri yorumunu yapabiliriz.
4. ÇEYREK SAPMA
- Bir dağılımda puanlar sıraya dizildiğinde %25. Dilimdeki puan ile %75.dilimdeki puanlar arasındaki farklılaşmanın bilgisini verir.
- Uç değerlerden etkilenmez.
- Bir dağılımda uç değer yokken en iyi merkezi eğilim ölçüsü, aritmetik ortalama dağılım ölçüsü, standart sapmadır.
- Uç değerler varken en iyi merkezi eğilim ölçüsü medyandır dağılım ölçüsü, medyandır.
ÇEYREK SAPMA (Q) = Q75- Q25/2 formülü ile bulunur.
D. STANDART PUANLAR (Z ve T Puanları)
- Hem simetrik dağılım hem de farklılaşmanın normal düzeyde olduğu dağılımdır.
- Bir dağılımın normal olabilmesi için çarpıklık katsayısının sıfır olması gerekir.
- Bir öğrencinin içinde bulunduğu gruptaki başarı sırası, yüzdelik dilimi, hangi derste başarılı ya da hangi derste başarısız olduğunu gösteren bağıl puanlamaya denir.
Z Puanı = X – Aritmetik Ortalama/Standart Sapma formülü ile bulunur.
- Z PUAN, grubun A.O =0 , S.S=1 olan dağılımdır.
- Öğrenci Z=0, üstünde puan almışsa başarılı
- Öğrenci Z=0, altında puan almışsa başarısız
- Öğrenci Z=0 ,eşit puan almışsa grubun yarısından başarılı, yarısından başarısızdır. Aynı zamanda grubun A.O’ na eşit puan almıştır denir.
- T PUAN; grubun Aritmetik Ortalaması=50 , Standart Sapması=10 olan dağılımdır.
- T puan , Z’ye bağlı hesaplanır.
- T Puanı = (10*Z) +50 formülü ile bulunur.
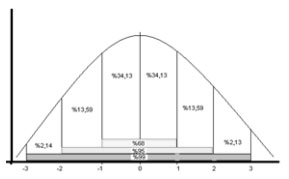
NOT: SİMETRİK DAĞILIM DEĞERLERİ

ÖRNEK 1: Ali‘nin gruba göre en başarılı olduğu test hangisidir?


Bu tarz sorularda önce Z puanını bulmak gerekir.
- 1. testin Z puanı: 70-60=10, 10/10=1 demek ki Z Puanı=1 çıkacaktır.
- 2. testin Z puanı: 50-30=20, 20/15= 1.3, Z Puanı=1.3
- 3. testin Z puanı: 90-85=5, 5/10= 0.5, Z Puanı: 0.5
- 4. testin Z puanı: 65-65=0, 0/7=0, Z puanı: 0
- Z puanı ne kadar yüksekse o testteki başarı daha fazladır. Bu durumda 2. testteki başarı daha fazladır.
ÖRNEK 2: Bir aday, şans başarısı düzeltme formülü kullanılmayan ve bağıl değerlendirme yapılan bu testlerin her birinde 40 soruyu doğru cevaplamışsa, adayın en başarısız olduğu test hangisidir?


- 40 soruyu doğru cevaplamışsa 40 puan aldığı yorumunu yapabiliriz.
- Formülümüz yine aynı Z puanı: Alınan puan – Aritmetik ortalama / Standart Sapma
- Felsefe için; 40-15= 25, 25/5= 5 = Z puanı
- Fizik için; 40-60=-20, -20/15= -1,33 = Z puanı
- Kimya için; 40-25= 15, 15/10= 1,5 = Z puanı
- Biyoloji için, 40-20= 20, 20/4= 5 = Z puanı
- Tarih için; 40-40=0, 0/15= 0 = Z puanı
- Z puanlarını değerlendirdiğimizde eksi Z puanında olan Fizik dersi en başarısız olunan, 5 Z puanına sahip olan Biyoloji dersi en başarılı olunan derstir.
D. MADDE ANALİZLERİ
1. MADDE GÜÇLÜK İNDEKSİ (p-pj-pjx)
- Bir maddeye doğru cevap verenlerin yüzdesidir.
- Bir maddeye doğru cevap verenlerin oranıdır.
- Bir testte yer alan maddenin kolay ya da zor olduğu hakkında bilgi verir.
- P= Doğru Cevap Veren Öğrenci Sayısı Toplam Öğrenci
MADDE GÜÇLÜK İNDEKSİ YORUMU
- (0 ve 1 ) aralığında yer alır.
- 0-0.40 arası ise madde zor
- 0.40-0.60 arası ise madde orta güçlük
- 0.60- 1 arası ise madde kolay
Güçlüklerine Göre Madde Seçerken;
- Seçme-yerleştirme testlerinde: 0’a yakın
- Sınava katılan çok alım az ise: 0’a yakın
- En başarılı öğrenciler: 0’a yakın
- Başarı testleri: 0.50
- İzleme testlerinde ise: 1’e yakın
- En başarısız öğrenciler: 1’e yakın olmalıdır.
ÖRNEK: Bir testin 6. Maddesine 50 öğrenciden 15 tanesi doğru cevap vermiştir. Maddenin güçlüğü hakkında neler söylenebilir ?
ÜST GRUP-ALT GRUP TABLOLARINDA GÜÇLÜK
P = (Dü+Da)/Toplam Öğrenci Sayısı formülü kullanılır.
Dü: Üst grupta doğru cevap verenlerin sayısı
Da: Alt grupta doğru cevap verenlerin sayısı
ÖRNEK 1: 3. Maddenin güçlük indeksi nedir ?


- Formülümüzü uygulamadan önce doğru cevabı tespit etmeliyiz. Doğru cevap üst gruptakilerin en çok işaretlediği C şıkkıdır.
- Şimdi formülümüzü uygulayabiliriz; Dü=50, Da=10, 50+10=60, şimdi bu sayıyı toplam öğrenci sayısına böleceğiz. 60/ 240= 0.25. Madde güçlük indeksi = 0.25’tir.
ÖRNEK 2: 15. Maddenin güçlük indeksi nedir ?


- Bir önceki sorudaki mantığı uyguluyoruz. Doğru cevabımız üst grubun yoğunlukla işaretlediği A şıkkı diyebiliriz.
- 40+20= 60, 60/200= 0,3 madde güçlük indeksimiz olacaktır.
- Doğru cevabın D olma durumunu ele alarak soruyu yine aynı şekilde cevaplayacağız.
- 30+10= 40, 40/200= 0,2 madde güçlük indeksini bulabiliriz.
2. MADDE AYIRICILIK İNDEKSİ (r-rj-rjx)
- Bir maddenin bilenle bilmeyeni ayırt etme derecesini gösterir.
- Madde ayırıcılık indeksi, r= Dü-Da/n (toplam grup sayısının yarısı) formülü ile bulunur.
AYIRICILIK YORUMU
- (-1 ve +1) aralığında değer alır.
- (-) değer alırsa madde testten atılır (ters yönde ayırıcıdır)
- 0- 0.19 madde testten atılır ya da bütünüyle değiştirilebilir.
- 0.20-029 madde değiştirilmelidir.
- 0.30- 0.39 maddede ufak düzeltmeler yapılabilir.
- 0.40 ve üstü ideal ayırıcıdır.
ÖRNEK: 5. Maddenin ayırıcılık indeksi nedir ?


- Formülümüz belli, formülü uygulamadan önce A şıkkının doğru cevap olduğunu görüyoruz.
- Şimdi formülü uygulayabiliriz. 70+30=100, 100/100= 1 madde ayırıcılık indeksimiz 1 olarak bulundu.
- Bu durumda 0.40’ın üstünde çıkan madde ayırıcılık indeksi ideal ayırıcıdır.
3. DOĞRU CEVAP NASIL OLMALIDIR ?
- Bir maddenin doğru cevabı üst gruptakileri (bilenler) çekmeli, alt gruptaki (bilmeyenler)çekmemelidir.
- Bir maddenin ayırıcılık değerinin düşük çıkmasının nedeni, doğru cevap seçeneğinin ve çeldiricilerin görevini yerine getirememelerindendir.
4. ÇELDİRİCİLER
- Çeldirici doğru seçeneğin dışında kalan seçeneklere denir.
- Çeldiriciler gruptaki bilmeyen öğrencileri kandırır.
- Çeldiricilerde alt gruptakileri çekmelidir.
- Çeldiriciler, çeldiricilere düşen toplam öğrenci sayısını dengeli paylaşmalıdır. Aksi durumda zayıf ve kuvvetli çeldiriciler meydana gelir.
ZIT YÖNDE İŞLENMİŞ ÇELDİRİCİ (YANLIŞ,KÖTÜ)
- Üst grupta alt gruptan fazla sayıda öğrenci çeken çeldiricidir.
- Bu çeldiriciler, doğru cevaba öğrenci göndermeyeceğinden ayırt edicilik düşer.
ZAYIF ÇELDİRİCİ
- Alt ve üst grupta toplamda az sayıda kişiyi kendisine çeken çeldiricilerdir.
- Zayıf çeldiriciler yeterince çalışmayan çeldiricilerdir.
- Kolaylıkla elendiklerinden şans başarısını artırırlar.
KUVVETLİ (ETKİLİ) ÇELDİRİCİ
- Alt ve üst grupta toplamda çok sayıda kişiyi kendisine çeken çeldiricilerdir.
- Kuvvetli çeldiriciler, maddenin zorlaşmasına neden olurlar.
ÖRNEK: Çeldirici yorumlarını yapınız.


- (A doğru cevap )
- B çeldiricisi : Alt gruptan fazla ve üst gruptan az kişiyi kendine çektiği ve toplamda çok öğrenci çektiği için; Kuvvetli (Etkili) Çeldirici’dir.
- C çeldiricisi : Alt ve üst gruplardan az sayıda öğrenci çektiği için; Zayıf Çeldirici’dir.
- D çeldiricisi : Üst gruptan olan öğrencileri daha fazla çektiği için; Zıt Yönde (Yanlış – Kötü) Çeldirici’dir.
- E çeldiricisi : Alt gruptan fazla ve üst gruptan az kişiyi kendine çektiği ve toplamda çok öğrenci çektiği için; Kuvvetli (Etkili) Çeldirici’dir.
- Çeldiricileri en iyiden en kötüye sıralayınız: E>B>D>C olarak sıralanabilir.
5. MADDE STANDART SAPMA ve VARYANSI
- Bir maddenin doğru cevap oranı (p) ile aynı maddeye verilen yanlış cevap oranı (q) çarpımı, madde varyansıdır.
- p+q=1 olmalıdır.
- Madde Varyansı = p*q
- Madde varyansının alabileceği maximum değer 0.25’ tir.
- Bir maddenin standart sapması da varyansın karakökü kadardır.
- Standart sapmanın da alabileceği maximum değer 0.50’dir.
ÖRNEK: Doğru cevap oranları verilen değerlerin, yanlış cevap oranlarını, madde varyanslarını ve standart sapmalarını bulalım.
- P=0.20 q= 1-0.20 = 0.80 p*q= 0.80*0.20 = 0.16 SX= 0.16’nın karekökü = 0.4
- P=0.80 q= 1-0.80 = 0.20 p*q= 0.20*0.80 = 0.16 SX= 0.16’nın karekökü = 0.4
- P=0.50 q= 1-0.50 = 0.50 p*q= 0.50*0.50 = 0.25 SX= 0.25’in karekökü = 0.5
NOT: Bir madde kolay ya da zorlaştıkça ayırt ediciliği düşer. İdeal 0.50 güçlük, ideal varyans, standart sapmayı bulmayı sağlar.
6. MADDE GÜVENİRLİĞİ
- Bir maddenin güvenirlik değeri, o maddenin standart sapma (sx) değeri ve ayırıcılık indeksi (rx) değerlerinin çarpımıdır.
ÖRNEK 1: Hangi maddenin güvenirliği yüksektir ?


- Standart sapma * Ayırıcılık indeksi formülümüzü kullanarak 0.50*0.90= 0.45 diyerek en güvenilir maddenin 3. madde olduğunu söyleyebiliriz.
ÖRNEK 2: Hangi maddenin güvenirliğe katkısı en yüksektir ?


- Evet normalde böyle bir soruda “1-p” formülünü kullanarak “q” değerlerini bulup,
- Daha sonra “p*q” formülü ile varyansı bulup,
- Daha sonra varyansın karekökünü alarak standart sapmayı bulup,
- Standart sapma ile R değerini çarpmamız gerekirdi.
- Fakat bunların hiçbirini yapmadan şu bilgiyi aklımıza getireceğiz. Bir maddenin standart sapması en yüksek 0.5 olabilirdi. Bunun içinde q ve p değerlerinin de 0.5 olması gerekir. Bize bu işareti gösteren 3. maddedir. Ayrıca yine aralarında ki R değeri en büyük olan madde de 3. madde olduğuna göre hiç işlem yapmadan 3. maddenin en güvenilir madde olduğunu söyleyebiliriz.
7. MADDE MATRİSLER TABLOSU
- Matrisler tablosunda birler (1) doğru verilen cevabı, sıfırlar (0) yanlış cevabı işaret etmektedir.
- Satır ve sütunlardan oluşan bu tabloya bakarak bir çok konu hakkında yorum yapabiliriz.
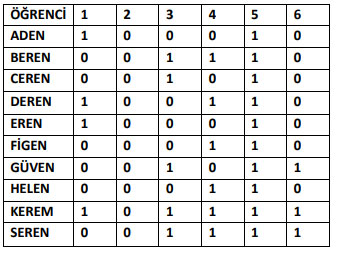

ÖRNEK: Soruları yukarıdaki tabloya göre cevaplayalım;
Öncelikle öğrendiğimiz gibi 1 doğru 0 yanlış diyerek gerekli hesaplamaları yapıp tüm sonuca ulaşabileceğiz.
a. Grubun mutlak başarısı en yüksek öğrenci:
- 5 adet doğru ile “KEREM” mutlak başarısı en yüksek öğrenci.
b. Grubun aritmetik ortalaması:
- Bu aşamada kişilerin puanlarını bulmamız gerekiyor.
- Aden: 2, Beren: 3, Ceren: 2, Deren: 3, Eren: 2, Figen: 2, Güven: 3, Helen: 2, Kerem: 5, Seren: 4 doğru yapmıştır.
- 2+3+2+3+2+2+3+2+5+4= 28 toplam doğru sayısı, bu sayıyı da kişi sayısına bölmemiz gerekiyor; 28/10=2.8 cevabına ulaşıyoruz.
c. Grubun modu:
- Grubun modu yani tepe değer, en çok tekrar eden puandır.
- Aden: 2, Beren: 3, Ceren: 2, Deren: 3, Eren: 2, Figen: 2, Güven: 3, Helen: 2, Kerem: 5, Seren: 4 bu puan dağılımında 5 kişinin 2 puan aldığını görüyoruz. En çok tekrar eden değerimiz 2 olduğundan mod da 2’dir.
d. Grubun medyanı:
- Puanları sıralamaya koymamız gerekiyor.
- 2,2,2,2,2,3,3,3,4,5 şeklinde sıraya koyulabilir.
- Medyan değeri puanlama sırasının ortanca değerine denir ve N/2 formülü ile bulunur.
- N değerimiz 10 kişi olduğundan 10’dur. 10/2=5 değeri medyan değerimizdir.
- Sondan ve baştan 5. sıraya bakıyoruz. Baştan 5. sırada “2 puan”, sondan 5. sırada ” 3 puanın” olduğunu görebiliriz.
- Daha önceki sorularda genelde aynı sayıyı buluyorduk. Bu sefer çıkan sayılarımız farklı olduğuna göre hesabı nasıl yapacağız?
- Eğer bir medyan hesabında sayılar farklı çıkarsa iki sayı toplanır ve ortalaması alınır.
- Bu durumda; 2+3=5, 5/2= 2.5 değeri medyan değerimiz olacaktır.
e. Testin ortalama güçlüğü:
- Testin ortalama güçlüğünü; Aritmetik Ortalama/Testten Alınabilecek En Yüksek Puan formülü ile buluruz.
- Testin ortalama güçlüğü 2.8/6=0,46 çıkacaktır.
- Güçlük yorumu yaparken güçlük değerinin 0.5 civarı olması testin normal olduğunu gösterir. 0’a doğru zor test, 1’e doğru kolay test yorumu yapabilir. Bizim testimiz orta seviye bir testtir.
f. Grubun grafiği:
- Grubun grafiğini; aritmetik ortalama, mod ve medyan değerlerini yerleştirerek bulabiliriz.
- Bu test için aritmetik ortalamamız; 2.8 – medyanımız; 2.5 ve modumuz; 2 olarak bulunmuştu.
- Aritmetik ortalama>Medyan>Mod dizilimi bize sağa çarpık dağılım grafiğini verecektir.


g. Grubun ranj değeri:
- Ranj değeri en yüksek nottan en düşük notun farkıdır.
- 5-2=3 ranj değerimiz olacaktır.
h. En zor madde:
- 6 maddenin doğru cevaplanma sayılarına bakacağız;
- 1. soru 4, 2. soru 0, 3. soru 5, 4. soru 6, 5. soru 10 ve 6. soru 3 doğru cevap almış.
- Bu durumda en az doğru yanıta sahip 2. soru en zor maddemiz olacaktır.
i. En kolay madde:
- Yine maddelere verilen doğru yanıtlara baktığımızda en fazla doğru yanıta sahip 5. soru en kolay maddemiz olacaktır.
j. Standart sapma ve varyansı en düşük madde:
- Normalde bu tarz sorularda standart sapma formülü olan (doğru cevap oranı)p*q(yanlış cevap oranı)=Varyans, ardından da bulduğumuz varyansın karekökünü alma işlemini kullanmalıyız.
- Fakat biliyoruz ki standart sapma farklılıkları gösteren bir değerdir. Bir soruya verilen doğru ve yanlış cevap sayılarının farklılığını gösterir. 5. soruda herkes doğru cevap verdiğine göre standart sapmamız 0 çıkacaktır. Yine aynı şekilde 2. soruda da tam ters olarak kimse doğru yanıt vermediğinden burada da standart sapma 0 çıkacaktır.
- Bu durumda varyans ve standart sapmanın en düşük olduğu madde 5. ve 2. maddelerdir.
k. Standart sapma ve varyans en yüksek madde:
- Yine bir önceki soruda verdiğimiz formülü kullanmamız gerekmektedir. Ama bir önceki soruda olduğu gibi basit bir yolla cevaplayacağız.
- Biliyoruz ki madde varyansının alabileceği en yüksek değer 0.25, standart sapmanın alabileceği en yüksek değer ise 0.50’dir. Bu da p ve q değerlerinin eşit olması durumunda ortaya çıkan sonuçtur.
- Bu durumda birbirine en yakın doğru yanlış değerine sahip sorunun 3. madde olduğunu görüyoruz.
- Standart sapma ve varyansın en yüksek olduğu madde 3. maddedir.
l. 2. Maddenin varyansı:
- 2. maddenin doğru yanlış oranlarına baktığımızda 0 doğru 10 yanlış olduğunu görüyoruz.
- p değerimiz 0, q değerimiz 1 oldu.
- 1*0=0, madde varyansımız 0 bulundu.
m. 2. Maddenin standart sapması:
- Standart sapma varyansın kareköküdür. 0’ın karekökü 0 olacağından standart sapmamız 0’dır.
n. 5. Maddenin varyansı:
- Önceki 2 soruda görülen nedenlerden olayı varyansımız 0 olacaktır.
o. 5. Maddenin standart sapması:
- Önceki 2 soruda görülen nedenlerden olayı standart sapmamız 0 olacaktır.
p. Geçerliğe ve güvenirliğe katkısı fazla olan:
- 3. maddenin standart sapması en yüksek olduğundan geçerliğe ve güvenirliğe etkisi en yüksektir.
r. Geçerliğe ve güvenirliğe katkısı az olan:
- 2 ve 5. maddelerin geçerliğe ve güvenirliğe etkisi en düşüktür.


